Line of Sight?
Why would Cherisey invent a publication written by an obscure priest called Cauneille entitled 'Line of Sight'? In what context would it be relevant in any way to the mystery he often writes about?
In Chapter XIII of his 1971 unpublished novel, Circuit, Cherisey reports on this book and he claims to have “copied” it in full as well as adding that there were also notes by a character called General David-Leroy.
He writes;
"Here therefore is the little work by the Abbé Cauneille, amplified by notes by General David-Leroy.
To my faithful servant and his descendants I bequeath these lines. May they throw them away when they cease to be of any interest. A copy of the whole text is in the possession of Monsieur de la Vauguyon, the French Ambassador to Spain.
THE FRENCH ZERO MERIDIAN".
We see straight away from this that the line of sight is about a Meridian, the French zero Meridian. As the document then lists towns along the Meridian, perhaps looking along the sight line of this particular Meridian is the order of the day?
But why should the 'whole' text be in the possession of one Monsieur de la Vauguyon?
Monsieur de la Vauguyon was a French politician, & peer of France, who served as a plenipotentiary minister and ambassador to Spain during the reign of Louis XVI. His father, Antoine de Quélen de Stuer de Caussade (a Breton family, from Porhoët for the Stuer). Porhoët [pɔʁwɛt] is a historical country in the center of Brittany, initially corresponding to the pagus trans sylvam ("outer-Forest" or Porhoët), around Mûr-de-Bretagne, which was a pagus, i.e. an administrative subdivision of the Domnonée, located on both sides of the Oust, a right bank tributary of the Vilaine. It was sparsely populated and heavily wooded, and is therefore sometimes associated with Brocéliande and Argoat. The Poutrocoët was also once a diocese. Until the 860s, bishops whose seat was in Aleth were generally called episcopus in Poutrocoet or episcopus in pago trans silvam, sometimes episcopus in Aleta civitate (bishop in the civitas of Aleth").
Around the year 1000, the Porhoët was a viscounty. The viscounty and then county of Porhoët appears in the 11th century, bringing together more than 140 parishes and covering nearly 4,000 km². Also known as Poher, it becomes a traditional country in Brittany located between the Monts d'Arrée and the Black Mountains, also called "Haute-Cornouaille" and designated, in recent decades, by the names Pays Centre Ouest Bretagne and Kreiz Breizh. The Poher was the seat of a powerful dynasty of counts in the Carolingian era, whose traces are scattered in the very rare archives and in the Lives of the Breton saints. Conomor (Kon Meur = Big Dog), noted as Prince of Poher, is bathed in a legend that makes him the Bluebeard of Brittany in the sixteenth century.
The name of Conomor is mentioned several times by Gregory of Tours as a Breton count who saves Macliauus from the vindication of his brother, the Count of Brittany, Chanao. He is also an opponent of the Franks welcoming Chramme, governor of Auvergne and son of Clotaire I. After a first revolt in 556, Clotaire I, the father of Chramme, forgave him this rebellion for the first time. In 559, Chramme revolted again, but defeated took refuge with Conomor, Count of Brittany in Vannes. He also appears at different times on the other side of the English Channel.
In 871, while Solomon was still king of Brittany, Judicaël was indicated as princeps Poucher without knowing what marked this uncommon dignity at the time. Mathuédoi (died before 936) was Count of Poher at the beginning of the 10th century. Son-in-law of the King of Brittany Alain I the Great, he is the father of the first Duke of Brittany, Alain Barbetorte. A Viscount of Poher, named Bernard, appears in the 11th century and his lineage seems to have been of particular interest to the Sainte-Croix Abbey of Quimperlé, thus seeming to take over from the Cornouaille dynasty which had acceded to ducal dignity since Hoël II in 1066.
Mathuédoï (died before 936) was Count of Poher (comes of Poher) at the beginning of the century. Of unknown origin, Mathuédoï marries one of the anonymous daughters of Alain I the Great, and he is involved in the dissensions born after the latter's death. After 924, he was forced into exile with his family. He is welcomed by the English king Æthelstan, and no longer leaves England. About ten years later, the same Æthelstan helped his godson, Alain Barbetorte, the son of Mathuédoï, in the reconquest of his throne, which will only be ducal and not royal, after expelling the Vikings out of Brittany.
We should also remember in the 1970s that the Prieure de Sion [as reported in Holy Blood Holy Grail] had become a modest cause celebre among certain people in France. There were a number of magazine articles and some newspaper coverage. On February 13th, 1973, the Midi Libre published a lengthy feature on Sion, Sauniere and the mystery of Rennes-le-Chateau. This feature specifically linked Sion with a possible survival of the Merovingian bloodline into the twentieth century. It also suggested that the Merovingian descendants included a 'true pretender to the throne of France', whom it identified as M. Alain Poher. .... As far as we know, M. Poher never commented, one way or the other, on his alleged connections with the Prieure de Sion and/or the Merovingian bloodline. In the genealogies of the 'Prieure documents', however, there is mention of Amaud, Count of Poher, who, sometime between 894 and 896, intermarried with the Plantard family - the direct descendants supposedly of Dagobert II. Amaud de Poher's grandson, Alain, became duke of Brittany in 937. Whether or not M. Poher acknowledges Sion, it would thus seem clear that Sion acknowledges him as being, at the very least, of Merovingian descent. [Holy Blood, Holy Grail].
Only recently did I realise that the line of sight might have something to do with reflections. Why? Because in many other publications both Cherisey and Plantard refer to these abstract ideas [in relation to Rennes]. In Stone & Paper Cherisey wrote;
"How many trips did we make, my friend Basil1 and me, in these nauseating passages until, one day, whilst musing better over the words BERGÈRE PAS DE TENTATION, the search seemed as fruitless to us as trying to grab the reflection of a treasure and take the shadow for prey. There was a temptation to which one should not succumb. If, at sunrise, the shepherdess was dazzled by the reflection of the gold, and not by the gold itself, it was because the sun was behind her and, therefore, she was looking west. Thus, it was more important to know where the shepherdess was2 than where she was looking. Asmodeus, the Devil who guards the church of Rennes-le-Château, confirmed this, "Anyone claiming to have seen the treasure of Asmodeus will never reach it since it is under one's feet". This is one of the reasons why, as keen as you are to find the treasure, you will find it reasonable that I stop at that. Not having the presumptuousness of considering myself more intelligent than the readers, I invite them to pursue the meditation about the mirror, and to consider with me how the stare and reflection are less important than going through the mirror3 and the anti-symmetrical phenomenon4 that opposes. As long as one is not trained to this gymnastic, it is no use going to Rennes-le-Château or even looking at the map; it is better to look at oneself in the mirror, with courage". [my emphasis].
And further;
"If you are looking for the treasure of Rennes-le-Château, ponder over the chess rules; at the start of a game, the queen is on her colour, whilst the king is on the colour opposite to his own. The king and queen represent the germ of dissymmetry in symmetry"5. [my emphasis].
And;
"An allusion to the legend of Labouisse-Rochefort in Voyage à Rennes-les-Bains, published in 1832. The Devil's gold is a musing over the mirror involving the stare and reflection6; "I am looking for the Devil's gold treasure from the legend to which I refer, and I will leave it at that." Anticipating the quest is crossing the mirror. Hence, the importance of asymmetry. [my emphasis].
And Pierre Plantard, in addresses given at RLC, include the following in his various speeches;
"The symbolic walk (claudication in the past) respected by the initiate in the Priory of Sion, from number 1 to number 22 (from black to white), followed by number 22 to number 43 (from white to black), and finally number 43 to number 64 (from black to white), makes him an individual capable of covering the circuit of sixty-three leaps. This walk is done at right angles of three squares in every direction. There are three veils to lift, namely three passwords, to penetrate in the Arch. When the knight carries the rose, he must conquer the esoteric chessboard through a last gesture, by accomplishing the last leap of the 3rd leg, namely by returning from 64 to 1, or get over the time-space. Only then will the initiate become the "checkmate", the "fool", the "bishop", whose hat is the miter, "the cowl that covers the chimney"7. The twenty-two leaps of the last leg are also the twenty-two cards (major arcana) of the Tarot from Marseille. Only one author, Oswald Wirth, who was in fact initiated, understood this matter very well in one of his works [Le tarot des Imagiers du Moyen Age (The Tarot of Middle-Age Painters of Popular Pictures) written in 1927.]
This paragraph is presented with the following diagram;
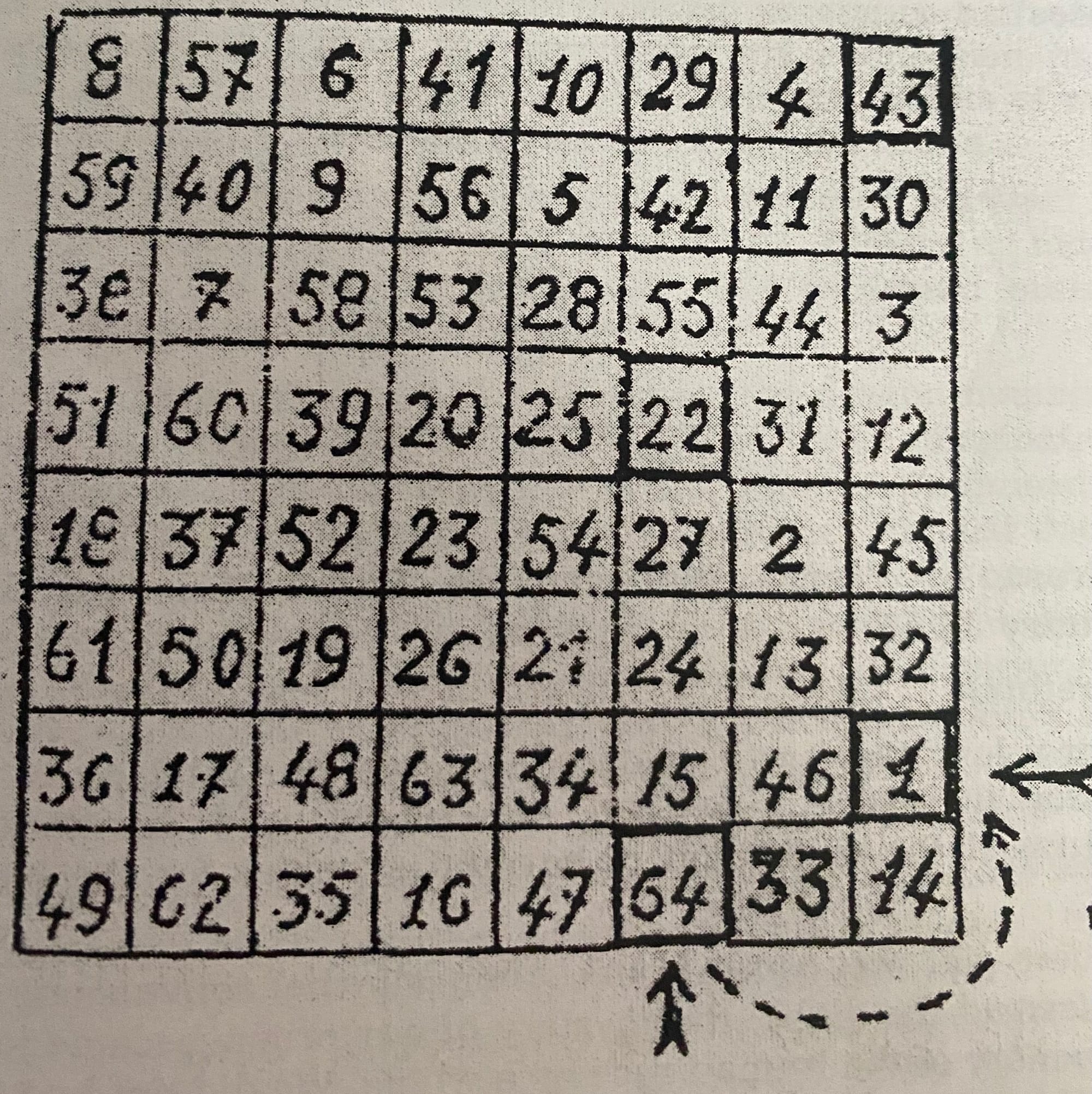
Then follows this;

which have correlates with the following from Plantard's Le Cercle;

&
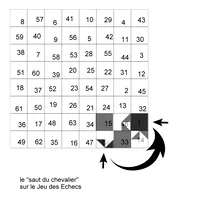
Only at this moment, the initiate becomes the "mat" or the "fool", "the bishop" whose bonnet is the mitra, "that covers the chimney". [Conference Plantard 6 Juin 1964, RLC], but there are only two doors for accomplishing this jump from 64 to 1, (equerre) the square of 14 (temperance) or the square of 15 (the devil) according to the 22 arcanas of the TAROT de Marseille (Marceille) [Le Cercle page 75]

So what do all these terms Plantard and Cherisey refer to? And how are we to apply it all in relation to 'a tresor a Rennes'? [I gathered all the descriptions below mainly from wikipedia!]
The Line of Sight refers to the straight path that light travels from an observer's eye to an object they are looking at. It's essentially the direction of view, and anything blocking this path can obstruct the view. In simpler terms, it's the path you see when you look at something. Here's a more detailed breakdown:
Imaginary Line: It's not a physical line, but an imaginary one that extends from the viewer's eye to the object of focus.
Straight Path: Light travels in a straight line, so the line of sight is also a straight line (unless affected by refraction or reflection, as in optics).
The concept of line of sight is important in various fields, including:
- Vision: How we see objects in our environment.
- Navigation: Determining where to go and what to look for.
- Architecture: Designing buildings and spaces with optimal views.
- Surveying: Measuring distances and angles.
The term "line" typically presumes that the light by which the observed object is seen travels as a straight ray, which is sometimes not the case as light can take a curved/angulated path when reflected from a mirror, refracted by a lens or density changes in the traversed media, or deflected by a gravitational field. Fields of study feature specific targets, such as vessels in navigation, marker flags or natural features in surveying, celestial objects in astronomy, and so on. To have optimal observational outcome, it is preferable to have a completely unobstructed sightline.
In geometry, a ray is a part of a line that has one endpoint and extends infinitely in one direction. In optics, a ray of light is an idealized representation of the path of light, depicted as a straight line perpendicular to the wavefronts. These rays are used to simplify the illustration and analysis of light's behaviour, such as reflection and refraction.
The idea on the front of the Cauneille book is also a rayon de miel which translates to "honeycomb" in French, and refers to a hexagonal shape inspired by the structure of a honeycomb. The Honeycomb Structure: is the hexagonal shape, mirroring the cells in a honeycomb. You can see this design faintly on the Caunielle alleged book and there is also a bee present;
A common experiment in sciences classes to illustrates these points involves the determination of the image location of a pencil as formed by a plane mirror. In the process of determining the image location, the manner in which light from the object travels to your eye is investigated. First, the method of parallax is used to locate the image of the object. Two pencils are inserted into rubber stoppers; one stoppered pencil serves as the object and the other serves to assist the student in locating the image. The object pencil is placed in front of a plane mirror. Then the student sights at the image of the object pencil in the mirror. As a student sights along a line (the line of sight) at the image of the pencil, the second pencil is placed behind the mirror along the same line of sight; this is called the image pencil. When placed along the line of sight, the portion of the image pencil that extends above the mirror will be aligned with the image that is seen in the mirror. Then the eye location is repositioned to the other side of the object pencil and the process is repeated. The precise image location of the object is the location where all lines of sight intersect regardless of where the eye is located.
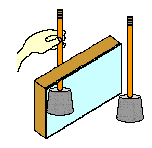
Two important ideas are gleaned from such a lab test: one pertains to how light travels from the object to the eye and one pertains to the location of the image of an object. As you sight at the image of an object in the mirror (whether it be a stoppered pencil or any object), light travels along your line of sight towards your eye. The object is being illuminated by light in the room; a countless number of rays of light are reflecting off the object in a variety of directions. When viewing the image of the object in a plane mirror, one of these rays of light originates at the object location and first travels along a line towards the mirror.
This ray of light is known as the incident ray - the light ray approaching the mirror. The incident ray intersects the mirror at the same location where your line of sight intersects the mirror. The light ray then reflects off the mirror and travels to your eye (as represented by the red ray in the diagram below); this ray of light is known as the reflected ray.
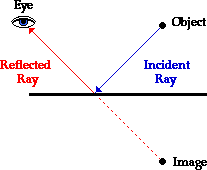
So the manner in which light travels to your eye as you view the image of an object in a mirror can be summarized as follows.
To view the image of an object in a mirror, you must sight along a line at the image. One of the many rays of light from the object will approach the mirror and reflect along your line of sight to your eye.
The second important idea that can be gleaned from this stoppered pencil lab pertains to the location of the image. Observe in the diagram above that the image is positioned directly across the mirror along a line that runs perpendicular to the mirror. The distance from the mirror to the object (known as the object distance) is equal to the distance from the mirror to the image (known as the image distance). For all plane mirrors, this equality holds true:
The bottom line is: without light, there would be no sight. The visual ability of humans and other animals is the result of the complex interaction of light, eyes and brain. We are able to see because light from an object can move through space and reach our eyes. Once light reaches our eyes, signals are sent to our brain, and our brain deciphers the information in order to detect the appearance, location and movement of the objects we are sighting at. The whole process, as complex as it is, would not be possible if it were not for the presence of light. Without light, there would be no sight.
In the phrase the 'line of sight'
The objects that we see can be placed into one of two categories: luminous objects and illuminated objects. Luminous objects are objects that generate their own light. Illuminated objects are objects that are capable of reflecting light to our eyes. The sun is an example of a luminous object, while the moon is an illuminated object. During the day, the sun generates sufficient light to illuminate objects on Earth. The blue skies, the white clouds, the green grass, the colored leaves of fall, the neighbor's house, and the car approaching the intersection are all seen as a result of light from the sun (the luminous object) reflecting off the illuminated objects and traveling to our eyes. Without the light from the luminous objects, these illuminated objects would not be seen.
During the evening when the Earth has rotated to a position where the light from the sun can no longer reach our part of the Earth (due to its inability to bend around the spherical shape of the Earth), objects on Earth appear black (or at least so dark that we could say they are nearly black). In the absence of a porch light or a street light, the neighbour's house can no longer be seen; the grass is no longer green, but rather black; the leaves on the trees are dark; and were it not for the headlights of the car, it would not be seen approaching the intersection. Without luminous objects generating light that propagates through space to illuminate non-luminous objects, those non-luminous objects cannot bee seen. Without light, there would be no sight.
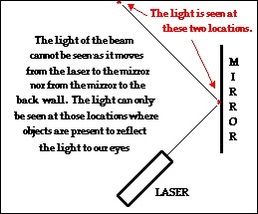
A common Physics demonstration involves the directing of a laser beam across the room. With the room lights off, the laser is turned on and its beam is directed towards a plane mirror. The presence of the light beam cannot be detected as it travels towards the mirror. Furthermore, the light beam cannot be detected after reflecting off the mirror and traveling through the air towards a wall in the room. The only locations where the presence of the light beam can be detected are at the location where the light beam strikes the mirror and at the location where the light beam strikes a wall. At these two locations, a portion of the light in the beam is reflecting off the objects (the mirror and the wall) and traveling towards the students' eyes. And since the detection of objects is dependent upon light traveling from that object to the eye, these are the only two locations where one can detect the light beam. But in between the laser and the mirror, the light beam cannot be detected. There is nothing present in the region between the laser and the mirror that is capable of reflecting the light of the beam to students' eyes.
Light is known to behave in a very predictable manner. If a ray of light could be observed approaching and reflecting off of a flat mirror, then the behavior of the light as it reflects would follow a predictable law known as the law of reflection. The diagram below illustrates the law of reflection.
The ray of light approaching the mirror is known as the incident ray. The ray of light that leaves the mirror is known as the reflected ray. At the point of incidence where the ray strikes the mirror, a line can be drawn perpendicular to the surface of the mirror. This line is known as a normal line. The normal line divides the angle between the incident ray and the reflected ray into two equal angles. The angle between the incident ray and the normal is known as the angle of incidence. The angle between the reflected ray and the normal is known as the angle of reflection. (These two angles are labeled with the Greek letter "theta" accompanied by a subscript; read as "theta-i" for angle of incidence and "theta-r" for angle of reflection.) The law of reflection states that when a ray of light reflects off a surface, the angle of incidence is equal to the angle of reflection.
When a ray of light strikes a plane mirror, the light ray reflects off the mirror. Reflection involves a change in direction of the light ray. The convention used to express the direction of a light ray is to indicate the angle which the light ray makes with a normal line drawn to the surface of the mirror. The angle of incidence is the angle between this normal line and the incident ray; the angle of reflection is the angle between this normal line and the reflected ray. According to the law of reflection, the angle of incidence equals the angle of reflection. These concepts are illustrated in the animation below.
It is common to observe this law at work in a Physics lab such as the one described in the previous part. To view an image of a pencil in a mirror, you must sight along a line at the image location. As you sight at the image, light travels to your eye along the path shown in the diagram below. The diagram shows that the light reflects off the mirror in such a manner that the angle of incidence is equal to the angle of reflection.
It just so happens that the light that travels along the line of sight to your eye follows the law of reflection. If you were to sight along a line at a different location than the image location, it would be impossible for a ray of light to come from the object, reflect off the mirror according to the law of reflection, and subsequently travel to your eye. Only when you sight at the image, does light from the object reflect off the mirror in accordance with the law of reflection and travel to your eye.
Reflection - the image of something in a mirror or on any reflective surface: Reflection can refer to the bouncing back of waves, including light and sound, from a surface. In physics, reflection is the change in direction of a wavefront when it encounters a surface and returns into the medium it came from.
Reflection in Physics: the phenomenon where waves, like light or sound, bounce off a surface and return into the medium they were traveling in.
- Types of Reflection:
- Specular reflection: Occurs when light bounces off a smooth, shiny surface like a mirror, at the same angle it hit the surface.
- Diffuse reflection: Occurs when light bounces off a rough surface, scattering in different directions.
Mirror - A mirror, also known as a looking glass, is an object that reflects an image. Light that bounces off a mirror forms an image of whatever is in front of it, which is then focused through the lens of the eye or a camera. Mirrors reverse the direction of light at an angle equal to its incidence. This allows the viewer to see themselves or objects behind them, or even objects that are at an angle from them but out of their field of view, such as around a corner. Natural mirrors have existed since prehistoric times, such as the surface of water, but people have been manufacturing mirrors out of a variety of materials for thousands of years, like stone, metals, and glass. In modern mirrors, metals like silver or aluminium are often used due to their high reflectivity, applied as a thin coating on glass because of its naturally smooth and very hard surface.
A mirror is a wave reflector. Light consists of waves, and when light waves reflect from the flat surface of a mirror, those waves retain the same degree of curvature and vergence, in an equal yet opposite direction, as the original waves. This allows the waves to form an image when they are focused through a lens, just as if the waves had originated from the direction of the mirror. The light can also be pictured as rays (imaginary lines radiating from the light source, that are always perpendicular to the waves). These rays are reflected at an equal yet opposite angle from which they strike the mirror (incident light). This property, called specular reflection, distinguishes a mirror from objects that diffuse light, breaking up the wave and scattering it in many directions (such as flat-white paint). Thus, a mirror can be any surface in which the texture or roughness of the surface is smaller (smoother) than the wavelength of the waves.
When looking at a mirror, one will see a mirror image or reflected image of objects in the environment, formed by light emitted or scattered by them and reflected by the mirror towards one's eyes. This effect gives the illusion that those objects are behind the mirror, or (sometimes) in front of it. When the surface is not flat, a mirror may behave like a reflecting lens. A plane mirror yields a real-looking undistorted image, while a curved mirror may distort, magnify, or reduce the image in various ways, while keeping the lines, contrast, sharpness, colors, and other image properties intact
Staring is a prolonged gaze or fixed look. In staring, one subject or person is the continual focus of visual interest, for a long amount of time. Staring conceptually also implies confronting the inevitable – 'staring death in the face', or 'staring into the abyss'. In their 1995 paper published in Perception, von Grünau and Anston demonstrated that staring eyes (straight gaze with iris and pupilin center position in eye socket) are detected faster than eyes gazing to the right or left (averted gaze with iris and pupil in right-most or left-most position in eye socket). Eye targets with a straight gaze, when presented in an array of averted gaze non-targets, are detected faster with fewer errors than an averted gaze targets presented in an array of straight gaze targets. This search asymmetry, in which straight gaze targets are given preference in an array of averted gaze distractors, is found for both realistically drawn and schematic eye stimuli but not for other arrayed objects. Search asymmetry is not seen with geometric stimuli—for instance 1 x 3 rows of black and white squares—that vary in the position of the distinguishing feature, or stimuli consisting of only one schematic eye.
Going through a mirror, in the literal sense, is not possible as mirrors are designed to reflect light, not allow passage through them. However, there are figurative interpretations and fictional portrayals of "going through the mirror" that involve concepts like entering another dimension, a dream world, or engaging in introspection.
Literal Interpretation: Mirrors work by reflecting light due to their smooth, reflective surface. There is no known mechanism or scientific basis for physically passing through a mirror.
Figurative Interpretations and Fictional Portrayals:
Another Dimension/World: Some stories and works of fiction, like the Mickey Mouse cartoon "Thru the Mirror," depict characters entering another dimension or a topsy-turvy world by passing through a mirror.
Dream World: In some cases, "going through the mirror" is associated with entering a dream state or a surreal, dreamlike reality.
Introspection/Self-Reflection: The phrase "look in the mirror" is often used metaphorically to encourage self-reflection, introspection, and acknowledging one's own flaws or role in a situation.
While physically passing through a mirror is not possible, the concept of "going through the mirror" is often used in storytelling and psychological contexts to explore themes of other dimensions, dreams, self-reflection, and psychological conditions.
Asymmetry - In mathematics, an antisymmetric relation is a type of binary relation where, if two distinct elements are related in both directions, then the elements must be identical. More formally, a relation R on a set S is antisymmetric if for all elements an and b in S, if aRb and bRa, then a must be equal to b.
Here's a breakdown: Antisymmetric vs. Symmetric:
While symmetry means that if aRb, then bRa, antisymmetry is different. It doesn't mean the opposite of symmetry; rather, it means that if both aRb and bRa hold, then an and b must be the same element.
A relation is asymmetric if and only if it is both antisymmetric and irreflexive.
Symmetry, in general, refers to a sense of harmonious and balanced proportions, where one side or part mirrors or matches another. In mathematics, it specifically refers to an object's invariance under certain transformations like reflection, rotation, or translation. A shape is considered symmetrical if a line can be drawn through it, and either side is a reflection of the other, known as a line of symmetry.
Types of Symmetry:
Reflectional Symmetry (Line Symmetry/Mirror Symmetry): A shape has this symmetry if it can be folded along a line (line of symmetry) so that the two halves match perfectly.
Rotational Symmetry: A shape has this symmetry if it can be rotated around a central point and appear identical to its original position at least once before a full rotation.
Translational Symmetry: A shape has this symmetry if it can be shifted or moved without changing its appearance.
Glide Reflection Symmetry: This involves a combination of a reflection and a translation.
Symmetry in Different Contexts:
Geometry: Shapes can be symmetrical with varying numbers of lines of symmetry. For example, a square has four lines of symmetry.
Physics: Symmetry plays a fundamental role in understanding physical laws and phenomena, such as the symmetry of electric fields around charged objects.
Mathematics: Symmetry is a key concept in various mathematical fields, including group theory, where it's used to study symmetries of mathematical objects.
Asymmetry is the absence of, or a violation of, symmetry (the property of an object being invariant to a transformation, such as reflection). Symmetry is an important property of both physical and abstract systems and it may be displayed in precise terms or in more aesthetic terms. The absence of or violation of symmetry that are either expected or desired can have important consequences for a system.
In mathematics, asymmetry can arise in various ways. Examples include asymmetric relations, asymmetry of shapes in geometry, asymmetric graphs et cetera.
Lines of symmetry - When determining whether an object is asymmetrical, look for lines of symmetry. For instance, a square has four lines of symmetry, while a circle has infinite. If a shape has no lines of symmetry, then it is asymmetrical, but if an object has any lines of symmetry, it is symmetrical. Stated differently, an asymmetric relation is characterised by a necessary absence of symmetry of the relation in the opposite direction.
Asymmetry arises in physics in a number of different realms.
Thermodynamics - The original non-statistical formulation of thermodynamics was asymmetrical in time: it claimed that the entropy in a closed system can only increase with time. This was derived from the Second Law (any of the two, Clausius' or Lord Kelvin's statement can be used since they are equivalent) and using the Clausius' Theorem (see Kerson Huang ISBN 978-0471815181). The later theory of statistical mechanics, however, is symmetric in time. Although it states that a system significantly below maximum entropy is very likely to evolve towards higher entropy, it also states that such a system is very likely to have evolved from higher entropy.
Particle physics - Symmetry is one of the most powerful tools in particle physics, because it has become evident that practically all laws of nature originate in symmetries. Violations of symmetry therefore present theoretical and experimental puzzles that lead to a deeper understanding of nature. Asymmetries in experimental measurements also provide powerful handles that are often relatively free from background or systematic uncertainties.
Entropy is one of the few quantities in the physical sciences that requires a particular direction for time, sometimes called an arrow of time. As one goes "forward" in time, the second law of thermodynamics says, the entropy of an isolated system can increase, but not decrease. Thus, entropy measurement is a way of distinguishing the past from the future. In thermodynamic systems that are not isolated, local entropy can decrease over time, accompanied by a compensating entropy increase in the surroundings; examples include objects undergoing cooling, living systems, and the formation of typical crystals. Much like temperature, despite being an abstract concept, everyone has an intuitive sense of the effects of entropy. For example, it is often very easy to tell the difference between a video being played forwards or backwards. A video may depict a wood fire that melts a nearby ice block; played in reverse, it would show a puddle of water turning a cloud of smoke into unburnt wood and freezing itself in the process. Surprisingly, in either case, the vast majority of the laws of physics are not broken by these processes, with the second law of thermodynamics being one of the only exceptions. When a law of physics applies equally when time is reversed, it is said to show T-symmetry; in this case, entropy is what allows one to decide if the video described above is playing forwards or in reverse as intuitively we identify that only when played forwards the entropy of the scene is increasing. Because of the second law of thermodynamics, entropy prevents macroscopic processes showing T-symmetry.
lack of symmetry. the relationship between two objects when one is the mirror image of the other
"Crossing the mirror" can refer to several concepts, often involving a belief that mirrors act as portals or gateways to other realms. This can be interpreted literally in folklore and spirituality, where mirrors are seen as doorways for spirits or entities to enter our world. Alternatively, it can be a metaphorical expression, such as in religious contexts where "crossing the mirror" represents a transformation or shift in perspective, particularly when reflecting on one's own flaws or imperfections.
Here's a breakdown of the different interpretations:
1. Literal Interpretation (Folklore & Spiritual):Portals and gateways: In many cultures and folklore traditions, mirrors are believed to be magical devices that can reveal hidden things, act as portals to other dimensions, or allow spirits to pass between worlds.
Spirits and entities: Some believe that mirrors can attract or even be used by spirits, both benevolent and malevolent, to enter our reality.
Supernatural energies: Mirrors are thought to possess supernatural energies and can be used for scrying (divination) or other forms of communication with the spirit realm.
2. Metaphorical Interpretation (Spiritual & Religious): 'Crossing the mirror" can symbolize a deep examination of oneself, confronting one's flaws, and striving for personal growth.
Seeing oneself as God sees: In some Christian interpretations, "crossing the mirror" might refer to seeing oneself through the lens of God's grace and love, rather than through the lens of sin and imperfection.
Two-way mirror: The concept of a two-way mirror, where one side reflects one's own image and the other side reflects a different reality, can be used to illustrate the contrast between one's self-perception and how others (or God) perceive them.
The question "Get over Time-Space" is likely referring to the concept of time dilation in the context of space trave. Time dilation, a concept in Einstein's theory of relativity, describes how time can pass differently for observers in different frames of reference, particularly those moving at high speeds or experiencing strong gravitational fields.
Elaboration: Time Dilation:Einstein's theory of relativity explains that time is relative and not absolute. This means that the passage of time can be different for observers in different situations. Specifically, time slows down for objects moving at high speeds relative to a stationary observer, and it also slows down in regions with stronger gravitational fields.
Astronauts and Time: Astronauts on the ISS experience time dilation due to their high orbital velocity. While the effect is small (a few milliseconds over months), it's a real phenomenon predicted by relativity.
Space Travel and Time: The idea of time travel in the sense of going back to the past is highly speculative and not supported by current scientific understanding. However, forward time travel, or experiencing time at a different rate, is a well-understood phenomenon within the framework of relativity. In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualizing and understanding relativistic effects, such as how different observers perceive where and when events occur.
Until the turn of the 20th century, the assumption had been that the three-dimensional geometry of the universe (its description in terms of locations, shapes, distances, and directions) was distinct from time (the measurement of when events occur within the universe). However, space and time took on new meanings with the Lorentz transformation and special theory of relativity. In 1908, Hermann Minkowski presented a geometric interpretation of special relativity that fused time and the three spatial dimensions into a single four-dimensional continuum now known as Minkowski space. This interpretation proved vital to the general theory of relativity, wherein spacetime is curved by mass and energy. Non-relativistic classical mechanics treats time as a universal quantity of measurement that is uniform throughout, is separate from space, and is agreed on by all observers. Classical mechanics assumes that time has a constant rate of passage, independent of the observer's state of motion, or anything external. It assumes that space is Euclidean: it assumes that space follows the geometry of common sense.
In the context of special relativity, time cannot be separated from the three dimensions of space, because the observed rate at which time passes for an object depends on the object's velocity relative to the observer. General relativity provides an explanation of how gravitational fields can slow the passage of time for an object as seen by an observer outside the field. In ordinary space, a position is specified by three numbers, known as dimensions. In the Cartesian coordinate system, these are often called x, y and z. A point in spacetime is called an event, and requires four numbers to be specified: the three-dimensional location in space, plus the position in time (Fig. 1). An event is represented by a set of coordinates x, y, z and t. Spacetime is thus four-dimensional.
Unlike the analogies used in popular writings to explain events, such as firecrackers or sparks, mathematical events have zero duration and represent a single point in spacetime. Although it is possible to be in motion relative to the popping of a firecracker or a spark, it is not possible for an observer to be in motion relative to an event. The path of a particle through spacetime can be considered to be a sequence of events. The series of events can be linked together to form a curve that represents the particle's progress through spacetime. That path is called the particle's world line.
Time travel is the hypothetical activity of traveling into the past or future. Time travel is a concept in philosophy and fiction, particularly science fiction. In fiction, time travel is typically achieved through the use of a device known as a time machine. The idea of a time machine was popularized by H. G. Wells's 1895 novel The Time Machine.
It is uncertain whether time travel to the past would be physically possible. Such travel, if at all feasible, may give rise to questions of causality. Forward time travel, outside the usual sense of the perception of time, is an extensively observed phenomenon and is well understood within the framework of special relativity and general relativity. However, making one body advance or delay more than a few milliseconds compared to another body is not feasible with current technology. As for backward time travel, it is possible to find solutions in general relativity that allow for it, such as a rotating black hole. Traveling to an arbitrary point in spacetime has very limited support in theoretical physics, and is usually connected only with quantum mechanics or wormholes.
1] Pierre Plantard.
2] An allusion to Mount Serbairou - the legend is mentioned by Cherisey in the quote 'length of toises from the Greek Cross, on the ridge referred to by Boudet, 'bergere' also referred to the 'bonne colline' - the beautiful hill which is Mount Serbairou. This hill is itself associated with a shepherdess and treasure legend. The shepherdess wakes up early one day to see the Devil spreading his treasure in the sun. 'Toute la bonne colline en etait illuminee ['the entire beautiful hill was lit by it']. Cherisey said that, if at sunrise, the shepherdess was dazzled by the reflection of the gold, and not the gold itself, it was because the sun was behind her and therefore she was looking west. Thus it was important to know where the shepherdess was [Mount Serbairou] rather than where she was looking.
3] The concept of "going through the mirror" typically refers to either a physical impossibility, a psychological phenomenon, or a fictional narrative. While physically passing through a mirror is not possible due to the laws of physics, it can be a powerful metaphor in stories and a subject of psychological exploration. Mirrors reflect light, and the image you see is a result of light bouncing off your body and into your eyes. There's no physical space behind the mirror to step into, and no known way to alter the laws of physics to make this possible. Through the Looking-Glass":Lewis Carroll's sequel to Alice's Adventures in Wonderland features a world seen through a mirror, where logic is reversed and reality is altered. "Thru the Mirror":A 1936 Mickey Mouse cartoon where Mickey enters a mirror world and experiences a topsy-turvy version of his own life. Dreams:Mirrors in dreams are often symbolic and can represent self-perception, identity, or hidden aspects of the self. In essence, while physically passing through a mirror is not possible, the idea of "going through the mirror" can represent:A journey of self-discovery or transformation, A confrontation with one's inner self, A shift in perspective or understanding, and A fictional or dreamlike experience.2] A reference to Serbero.
7] A reference to Henri Boudet. 'The Pierre du Trou appears with honour on the mantelpieces of the chimneys, in the houses of our mountains". [ Boudet pag 256]